上篇谈到，可视化对于数据分析而言，是最基础但也重要的“探案”手段。一个优秀的数据分析师，可以从数据中读出很多“线索”。而所有的“线索”里，如果非要选一个最重要的，那正态分布毫无疑问就是解题最关键的一把钥匙。

为何正态分布如此常见和重要？

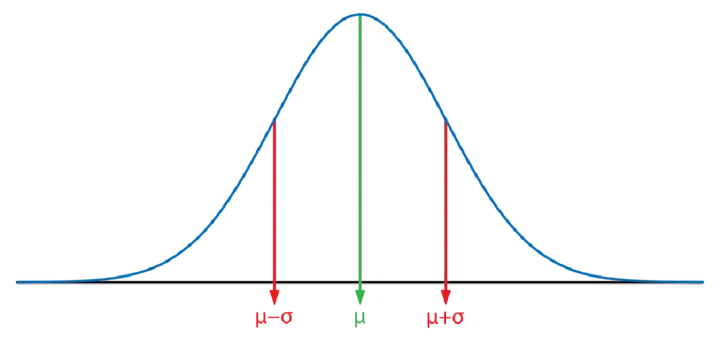
无论是大学的“概率与统计”课程，还是工业质量管理的“六西格玛”理论，都对正态分布进行了详细的讲解。正态分布也称为高斯分布，是一种在统计学中非常重要的概率分布，其概率密度函数如上图所示，呈钟形曲线，对称于均值。正态分布的特征由两个参数决定：均值（μ）和标准差（σ）。均值决定了分布的中心位置，而标准差决定了分布的宽度。正态分布的概率密度函数可以表示为：

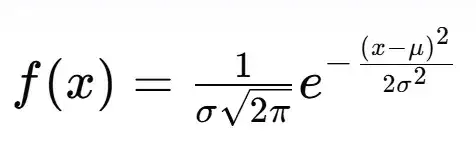
68-95-99.7规则：在正态分布中，大约68%的数据落在均值的一个标准差范围内，大约95%的数据落在均值的两个标准差范围内，大约99.7%的数据落在均值的三个标准差范围内。

在多年跨行业的实践中，我们也充分验证了正态分布无处不在，甚至有时候原始数据的正态分布形态非常完美，连仿真模拟都很难达到如此漂亮的形态。举个例子：假设很多台设备都生产一种零件，比如螺丝；每台设备的工艺参数、人工操作、尺寸测量都存在随机噪声，造成螺丝尺寸可能会有所不同。当把所有螺丝放在一起时，你会发现它们的尺寸分布就会呈现出一种中间高、两边低的形状，这就是正态分布的钟形曲线。

工业中正态分布之所以常见，与中心极限定理（Central Limit Theorem, CLT）有关。中心极限定理是一个统计学原理，它解释了在一定条件下，大量独立随机变量的和或平均值会趋向于正态分布，即使这些变量本身并不是正态分布的。也就是说，若一个工业现场的变量（如上例的螺丝尺寸）背后，是多个随机因素共同作用的共同结果，那该随机变量的分布就会自然趋向于正态分布！

如果不满足正态分布，意味着什么？

正态分布在工业现场是如此常见和重要，基于正态分布也就衍生出许多相应的分析手段，例如大学课程和六西格玛理论都有提到的“假设检验”，例如检验螺丝尺寸的均值是否偏离了原有的正态分布。但如果某个变量的数据分布不满足正态分布，那怎么办？

回顾上篇有关功耗的例子，我们通过数据分布的发现：·占比80%的主峰，基本符合正态分布，也是接下来分析建模的重点；·其他三个次峰，对应了三个不同的“工况”：一个是另一类子产品，两个是测量异常。

正态分布的产生是多个随机因素共同作用的结果。如果在某些关键变量：例如质量检测、设备负荷等数据上，数据明显呈现双峰或多峰分布，也就意味着多半有某个、或多个与此有关的关键因子“不随机”！因此，一条重要的分析线索就浮出水面——找到与双峰和多峰分布有关的因子，就可能解决某个生产现场的异常。

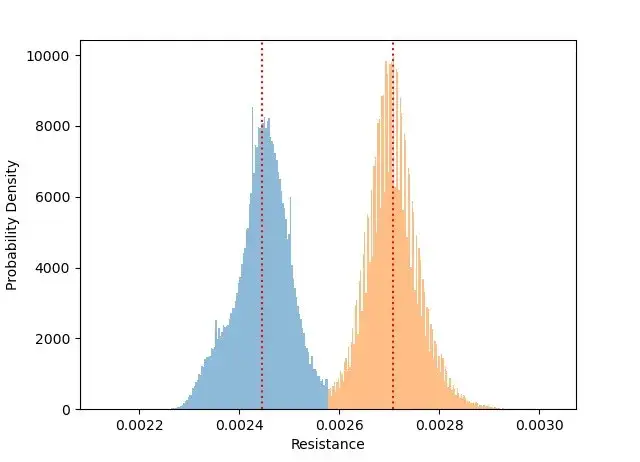
例如下图是某电路板产品的某个阻值的测量结果，很明显分成了0.0024和0.0027两个峰。熟悉六西格玛理论的可以知道，在这种情况下因为方差偏大，产品质量的CPK会明显变差！通过识别双峰的出现，并通过关联分析找到背后的原因，例如与某段工艺的某台设备有关，解决了该工艺段的设备差异性问题，该阻值恢复了单峰正态分布后，其CPK就会得到明显的改善！

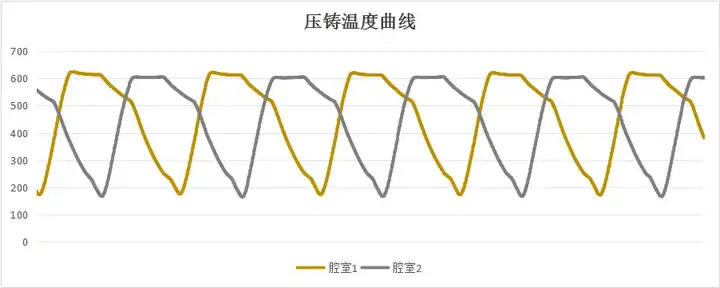
而下图是压铸机两个腔室的温度数据，温度曲线经历了“升温-稳温-降温”三个阶段，在稳温的最后时段通过模具对原料进行压铸，然后进行冷却。很自然想到，压铸前后的温度会对最终成品质量有较大关联性。

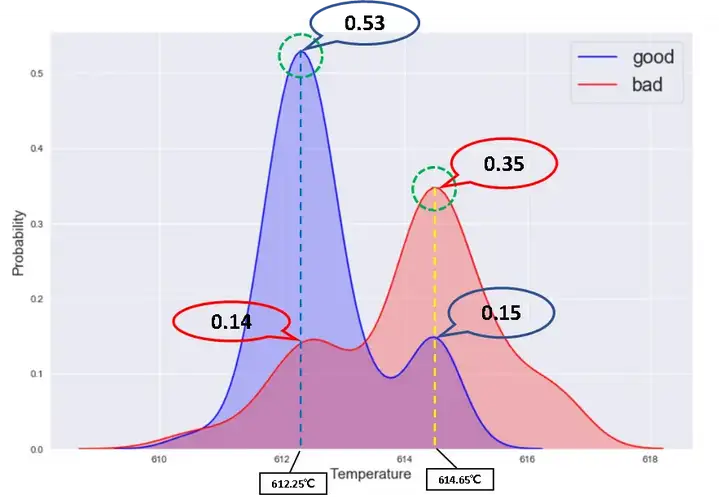
因此，通过加工“压铸时刻温度”这个特征，并将其与成品质量进行关联，可以得到下图的数据分布，从图上得知：

· 首先，当温度低于613.5度时，良品比例偏高；因此，建议现场设置613.5度作为报警温度，若压铸时刻温度超过613.5度，则良品率明显降低（该课题开展的过程中，的确发生过因为温度过高引起的批量质量事故）

· 其次，无论是良品还是不良品，都是双峰分布；且良品和不良品的双峰是重叠的，一个中心在612.25度，另一个中心在614.65度。这是一个重要的分析线索：除了温度之外背后还一定有另一个因子对于产品质量有影响！

接下来的问题是，如何猜测和分析双峰背后可能的原因。从业务逻辑和经验出发，我们可以梳理出两个潜在的下一步分析方向：

· 两个压铸腔室的温度传感器存在测量偏差，一个测量值偏高、一个测量偏低；

· 原材料存在批次间的差异，使得某一批的耐热性更好，另一批的耐热性较差。而这就将分析推向了下一个分析主题，一步步逼近问题的真相。

辛普森悖论：相关性反转

双峰或多峰问题对于接下来的分析建模所产生的影响可能是致命的，尤其是对于工业这类人造系统，背后都有强机理和强因果关系：也就是说每个数据现象，都一定有相应的因素！

定性来说，双峰或多峰的数据分布意味着其背后有至少一个关键、非随机因子的影响，它会使得原本基于正态分布假设的许多分析手法失效：例如CPK的计算失真，不能正确反映真实的产品质量情况，也不能帮助用户正确识别CPK降低的因素。严重的话，则会造成相关性反转，变量间的关系明显与机理、经验不符！

下图是一个经典的辛普森悖论的例子，横轴是每周锻炼时间，纵轴是生病概率。从经验上来说，锻炼多、身体好、生病概率应该低，所以锻炼时间和生病概率之间应该呈现负相关，但从下图可以看到其相关系数=0.33，是明显的正相关！难道是我们的日常经验错了吗？还是说，我们发现了新的科研成果？

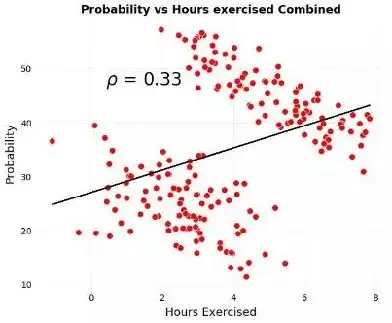
仔细点“看图说话”，我们发现数据分布呈现出明显的两个簇，也就是目前分析的两维数据呈现出了二维的双峰分布，这意味着背后应该存在着某个未知的非随机重要因子，可能影响到了“生病概率”这个目标变量。

当我们将这两个簇的数据分开分析，可以看到其分别的相关性呈现出来符合经验的“负相关”！再仔细分辨后，会发现两个簇数据所对应因子是“年龄”，50岁以下（左图）和50岁以上（右图），甚至50岁以上的负相关系数是大于50岁以上的，也就意味着对于年龄大的人锻炼是更有用的！这是符合常识的分析结论。

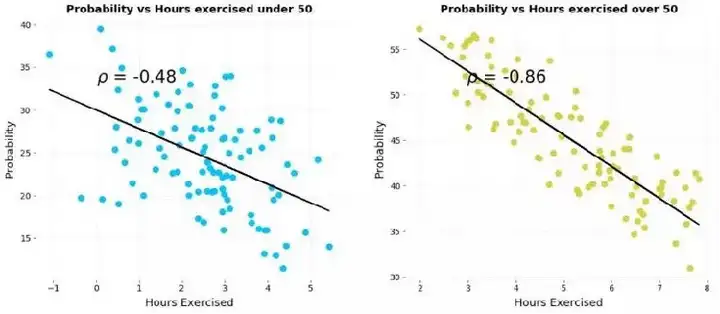
上图的例子本身是个极端情况，也是为了让读者更清楚看到：如果没有对正态分布或多峰分布进行识别，贸然采用一些分析建模的算法，可能会带来违背常识的结果。对于工业数据分析而言，我们强调过：因为其本身物理系统是个强机理、强因果系统，如果不加分辨的强行分析建模，往往会得到两类无用的结论：

· 不用数据分析，也是业务人员已知的确定关系：俗称重新发现牛顿定律；

· 通过数据分析，得到明显不符合业务的相关性结论：俗称推翻牛顿定律。而这两类数据分析结论，对于现场业务问题都是没有帮助的；另一方面，也是损害数据分析人员和算法的信誉的。

结语

在多年实践中，由正态分布所衍生出的分析手法：如何判别双峰/多峰，如何识别双峰/多峰的产生原因等，成为了众多工业数据分析领域的必备秘籍。双峰/多峰背后的原因，往往就是解决业务问题的第一把钥匙，使用领域包括并不限于：识别发电机组的负荷，分析质量问题背后的设备差异性，设备运行或生产工艺的工况切分等。

看图说话的下篇到此结束，一个重要的思想是：从数据现象里，通过综合应用可视化手段，可以发现许多数据背后的问题，成为工业数据分析破题的关键。

最后，我们留一个思考题给读者。欢迎留言互动！

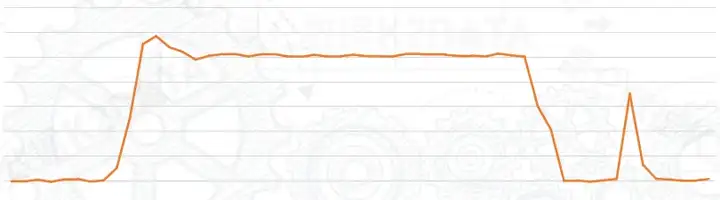
下图是某轧钢工艺的轧制力曲线，我们故意没有给出横轴和纵轴，原因是我们希望有一个通用的轧制工况识别的算法，也就是识别矩形波的区域，而忽略后续的干扰毛刺。因为该轧制工艺有多个因素影响轧制力的形态：

· 有多台轧机、多个道次，每个轧机和道次的轧制力大小和时长都不相同

· 有多类轧制的产品类型，不同产品类型的轧制力大小和时长也不同

· 有不同的钢材品类，使得其硬度和热性能也不一样

· 轧辊存在不同的工况状态，不同的直径组合，和不同时段的磨损程度

所面临的严峻问题是，在如此多、不可能穷尽的因素组合下，业务人员也无法对每个情形都去定义轧制力大小和时长的标准；那是否有相对通用的算法框架，可以适配如此复杂的情况，有效提取出轧制工况段（即矩形波区域）的数据特征？