首先，让我们回顾一下，数据探索的过程高度类似于福尔摩斯探案，大致的流程是：

• 通过数据分析手段，发现或发掘新的线索和证据（可视化分析就是一种发现新线索的常用方法）。

• 汇总目前已知的所有信息，包括已知的业务逻辑和数据线索，作为目前的证据链（就像破案时白板上杂乱的小贴士）。

• 通过逻辑推理识别目前证据链的缺漏或矛盾的地方，提出新的假设，即下一步探索破案的方向，进一步填补目前证据链。

• 结合业务逻辑，通过数据验证新的假设是否成立；必要的话，补充相关的业务知识和样例数据。

• 无论上述假设验证是否成立，都会形成一条新的线索；重复上述过程，直至证据链完备。

以下，将以三个案例将分享，如何在数据探索过程中，巧用假设验证，从蛛丝马迹中确认破题的关键。

案例1：利用自身统计特性

以上篇留下的思考题为例：如何提取轧制力的矩形波部分并计算特征；其核心问题是：

1. 不同轧机、不同道次、不同产品类型的轧制力大小和时长不定

2. 原始数据里存在各种噪声，如图中右边的毛刺

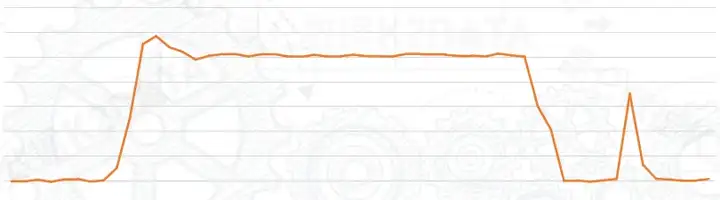
因此，问题的关键是：能否提取出矩形波部分和上升/下降过程及毛刺的不同特征，以便正确切分出矩形波区域。因此，我们提出如下假设：

• 矩形波区域（即实际轧制区域）的幅值和时长符合正态分布；

• 其它区域的幅值或时长不符合类似的数据分布特征。

例如，右侧毛刺的幅值可能很大（与矩形波区域接近），但其时长却明显的偏短。通过在样例数据上验证上述假设，我们就可以设置合适的滑动窗口大小，使用中位数滤波将毛刺区域识别和去除。

当然，上述假设验证只是整个问题解决的第一步，用来说明如何提出假设和验证的过程，并基于验证结论寻找解决方案（例如中位数滤波）。实际数据探索过程中，为了解决上篇提出的全部问题，还需要更多的子假设需要一一验证，并寻求相应的解决方案，例如：

• 不同产品类型、但同一轧机和道次的轧制力大小和时长是否符合同一正态分布？还是明显存在双峰/多峰分布？

• 同一轧机、同一道次，在不同时段是否符合相同的正态分布，还是存在随时间的劣化趋势？

案例2：由设备工况识别人的行为

某半导体封测企业希望借助数据分析来客观评价操作工的产出绩效。其困难在于：既无法用产量（如离散装配行业常用的计件），也无法用产品质量来评估其工作效果。因为其工作内容的复杂性很高：产品类型的不同、批次大小的不同、工序也不尽相同，这使得过往的绩效评估有较大的主观性，无法有效激励员工和识别有潜质的员工。

破题的关键在于找到“不变量”，经过和业务人员共同探讨，识别出操作工六大共同动作行为，如“报警响应”、“批次更换”等；而通过评价六大行为的效率和数量，就有可能形成一套完整且客观的产出绩效评估方法。将原始业务问题通过上述重构和转化是一个重大突破，也是本系列第一篇的主题：如何将业务问题进行数学建模；接下来就进一步拆解为如下问题：

• 是否有数据源可支持人的行为识别？

• 通过数据是否可以客观、准确的评价绩效？

第一个问题的答案相对清楚，我们由设备机台日志发现了非常完整的人工操作记录。通过定义操作工六大共同动作所对应的关键标志事件，从每台设备每天上万条日志记录里，可以识别出相应的动作信息：如“报警响应”对应的报警时刻和操作工的响应时刻，整体识别准确性在95%以上。下图是在样例数据上的动作行为识别结果展示，不同色带代表了不同行为的时段。

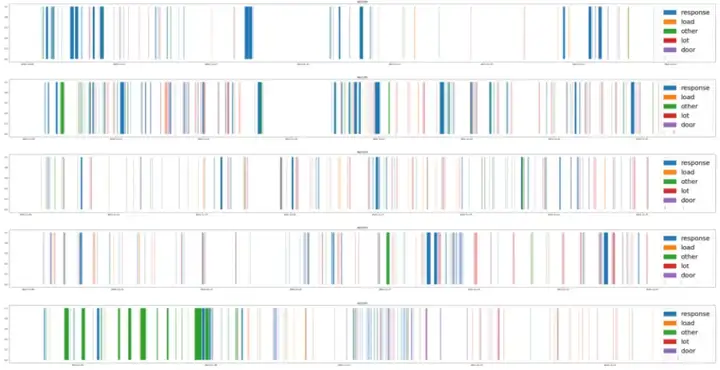
第二个问题则更有意思，例如同一个动作“报警响应”的时长，是否可以客观评价操作工的产出绩效呢？在此我们的假设是“二八原则”，也就是由某个指标评估（例如我们这里定义的动作时长）：大部分员工的表现差不多，少数的表现较差，也只有少数比较优秀。

基于上述动作行为的识别结果，统计了动作时长的分布图，例如下图是“报警响应”的时长统计。注意：这显然不是正态分布，报警响应时长的分布明显右偏且长尾：大部分在半分钟以内进行响应，但也有少量异常时长超过3分钟、甚至更长。但这样的时长分布恰好是我们期待的结果，因为根据排队论理论，对于“响应时长”这样的统计量，它理想的分布就应该是图中这样的“指数分布”！

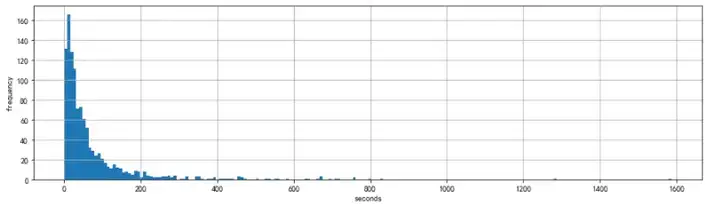
上图验证了我们的一个假设：报警响应时长的确符合预期的指数分布；下一个需要验证的假设就是：员工的差异性，是否能满足二八原则？这个假设的验证就相对容易，尝试将时长分布按照分位数对应到不同的绩效分数后，统计员工月度的均值，不意外的是：我们的确得到了近似正态分布的分数！

这个例子的巧妙之处既有业务层，也有技术层。业务上是在复杂的生产条件下找到了可能可以被用来客观评价的共性点；而技术上，则是基于排队论理论对于时长的分布假设，从数据中验证了该方向的可行性。整个过程比上文描述的复杂很多，但基本的逻辑和流程都是不断在业务上提出或大或小的假设，在数据上不断验证和调整思路的过程。最终这里呈现的结果，只是众多探索路径后，找到的那一条正确途径。

案例3：连续生产过程的复杂性

之前谈的大多属于离散或批次制造业的数据分析案例，一个优势是：基本上都有所谓的全局唯一物料ID，也就是某批或某个产品的所有生产工艺数据和质量检测数据，都可以通过唯一ID关联后进行分析。对于连续生产过程，却不具备这个ID进行数据关联，因而数据分析的第一步就会面临困难。

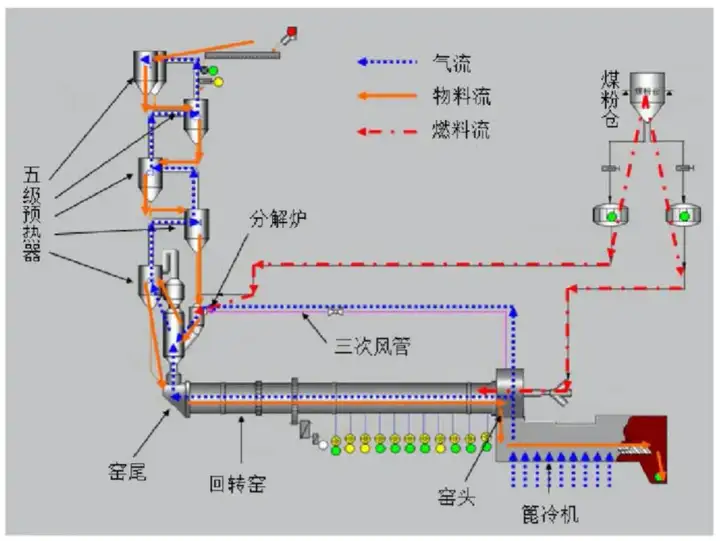
以上图的水泥生产过程为例，其主要工艺可以概括为三磨一烧，其中对成品质量影响较大的工艺环节主要是回转窑。这是一个典型的连续流程生产过程，原料从回转窑一端连续进入、生产过程是连续的、成品也是连续产出的。其中f-Cao（游离氧化钙）含量是水泥成品检测的一个重要指标，直接影响水泥质量。但是f-Cao的测量结果并不能实时获取，主要原因如下：

1. 原料在回转窑的进出需经过大约30分钟的时长（纯估算，没有办法精确测量；大部分的连续流程生产工艺都有类似的黑箱特点）；

2. 出窑后的成品经过篦冷机冷却，还需要大约20分钟左右到达末端；

3. 2小时一次在篦冷机末端提取检测样品送检，检测出结果还有数小时延迟。

因此，基于f-Cao检测结果控制回转窑的工艺参数，将面临很大的延迟，往不能及时调整相应工艺参数，等检测到f-Cao超标再调整就为时过晚，如下图是某水泥产线的f-Cao的测量结果，因为基于f-Cao检测结果反馈的人工调整偏晚，导致f-Cao大量超越管控限1.5%。

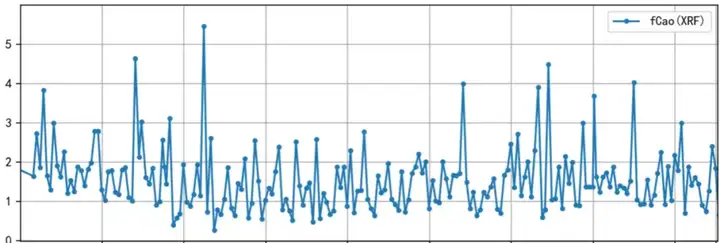
我们希望能用回转窑的工艺参数（X）来实时预测f-Cao含量（y），从而实现早期精准调控。然而，不假思索使用原始时序数据X和y进行建模，根本无法得到任何可靠的结果，X和y之间的相关性非常弱；算法层面的改进也基本无效，无法得到好的建模结果。

回顾本节开头提到的连续流程制造的一个困难是：没有公共ID进行精确关联，但并不意味不能构造一个合理的虚拟ID用来关联数据。注意到：检测时抽取的水泥样本，是大约50分钟前在回转窑中生产的，即当前化验得到的f-Cao含量y，应该是由50分钟前的回转窑工艺参数X所决定！因此，一个重要的假设就是：虽然原始X和y的相关性很弱，但y应该和大约50分钟前的X相关性较强。衍生的子假设是：因为回转窑是连续生产过程，状态也是连续变化的，且无法保障y都正好是50分钟前那一刻的X所唯一决定，因此对延迟50分钟附近的窗口（如10分钟）的工艺参数X进行滑动平均后，其相关性应该会进一步增强。

带着上述假设对原始数据进行滑动平均和延迟关联后，得到如下X和y的延迟相关性（以其中三个关键工艺参数为例），其中：横轴是时间延迟，纵轴是相关系数（绝对值越大，相关性越强），由图上可以得到的结论是：

• 非延迟关联情况下，原始X和y的相关性的确很弱

• 延迟相关性在110分钟时同时达到最大，三个关键参数和f-Cao都是负相关（与业务机理相符），而随后相关性又会变弱

• 按10分钟平滑后的相关性在同等条件下比不平滑的相关性更大

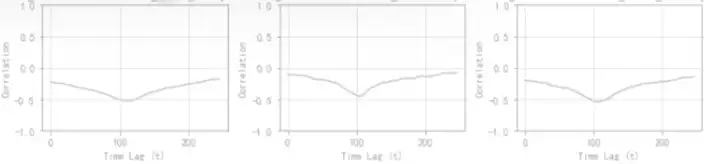
欣喜的是，数据的延迟相关性分析验证了我们的两个假设！但是，延迟相关性最大的点出现在110分钟，而非理论预期的50分钟，又是一个困惑的事情：难道是哪里的分析有问题，或是有什么未考虑到的因素影响？

而整个案例最精彩的是：用户完全认可了上述的延迟相关性的分析结论：110分钟而非50分钟的原因，是f-Cao数据的时区设置不对，恰好多了1小时！按照上述最优延迟相关性进行关联的X和y，基于样本数据和简单模型，就已经得到一个精度足够实用的实时f-Cao预测模型！随后的模型进一步改进，例如增加更多因素和样本、改进算法等，也都是在上述两个基本假设基础上开展。

结语

本篇的三个例子都是过去经验里比较有代表性的，也不止是讲述如何通过反复的“提出假设、验证假设”的过程，也正应了本系列第一篇的主旨：工业数据分析的破题关键，往往并不是在算法层面（算法基本都是最后一步了），而是在于如何有效结合业务和数据，从蛛丝马迹里寻找业务问题转化数学问题的关键。